
In case the ancient board game of Go is not complicated and challenging enough for you (it certainly is for me), here are some simple rules for playing Go on a four-dimensional Hypercube.
The HyperGo board
In the units of the Go board (in which the traditional board is of size 19x19), the Hypercube we will play on is of size 4x4x4x4 - we will call this the HyperGo board. This board might not seem very large, as a 4x4 sized conventional Go board would only produce very boring and short games. A 4x4x4x4 Hypercube however does have 256 points in it, which is not that much less than the 19x19=361 of the conventional Go board.
As four dimensions are generally rather hard to visualize, we map the positions of the Hypercube 'board' onto the traditional board, and there is a particularly nice way of doing this.
Consider the traditional 19x19 Go board:

Erase the lines defining rows and columns number 5, 10 and 15:

...and you are left with a 4x4 array of 4x4 Go boards.
This can be used as a representation of the HyperGo board. In four dimensions we have four orthogonal directions, x, y, z and w.
If we choose a particular point in one of the 16 4x4 squares, then we can move in the x- and y-directions by moving left/right and up/down inside the 4x4 square.
We can move in the z direction by jumping to the same x/y position in the 4x4 square to the left or the right. Imagine four of these 4x4 squares stacked into a three-dimensional cube. Then moving in the z direction is simply moving up and down vertically inside the cube.
Finally the movement in the w direction can be performed by jumping to the same x/y position in the 4x4 square above or below the original 4x4 square.
So you can move in four directions, but only at most four times until you hit the boundary of the hypercube, and therefore of the HyperGo board.
The HyperGo game
If you know Go, then the extension of the rules is straightforward:
1) Liberties are now the empty adjacent points in four dimensions, which means that a single stone on its own has eight liberties: (a) four in the conventional positions within its 4x4 square (above/below/left/right of the stone's position or less if there are boundaries) and (b) two above and below in the z direction, i.e. at the x/y position of the stone but on the 4x4 squares to the left and right, and (c) two 'above' and 'below' in the w direction, i.e. at the x/y position of the stone in the 4x4 squares above and below the original square. (Of course, if there is e.g. no 4x4 square above the one in which the stone lies, the stone lies on a boundary of the board in the w direction, etc.)
See the figure below for two examples of stones (o) and their liberties (x).
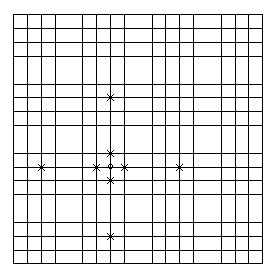
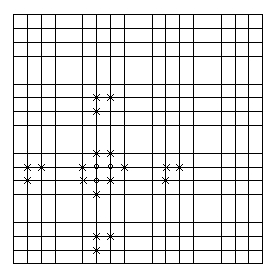
2) Chains can similarly be constructed in four dimensions, i.e. by placing stones on the same x/y coordinate in several 4x4 squares, which lie in a row or column of 4x4 squares. See below for an example of a four-dimensional chain structure.
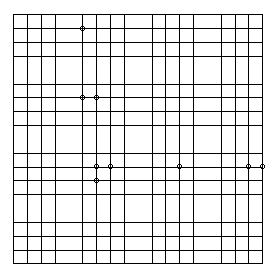
This is all you need to play HyperGo.
Why would I want to?
A very good question. Maybe because it gives one a chance to playfully explore four-dimensional space? Or maybe because normal Go is just way too easy... (Or maybe because you, like me, just seem to have too much spare time to think about stuff like this.)
S.E.A.